Autores: DUARTE, R. B. & M. B. S.
Introdução Link para o cabeçalho
Um reator contínuo de tanque agitado, ou CSTR, do inglês continuous stirred-tank reactor, é um tanque com agitação mecânica suficiente para que a mistura de seu conteúdo possa ser considerada perfeita, ou seja, a concentração é uniforme e não depende de coordenadas espaciais, quando o tanque é operado em regime permanente não há também a dependência da concentração com o tempo.
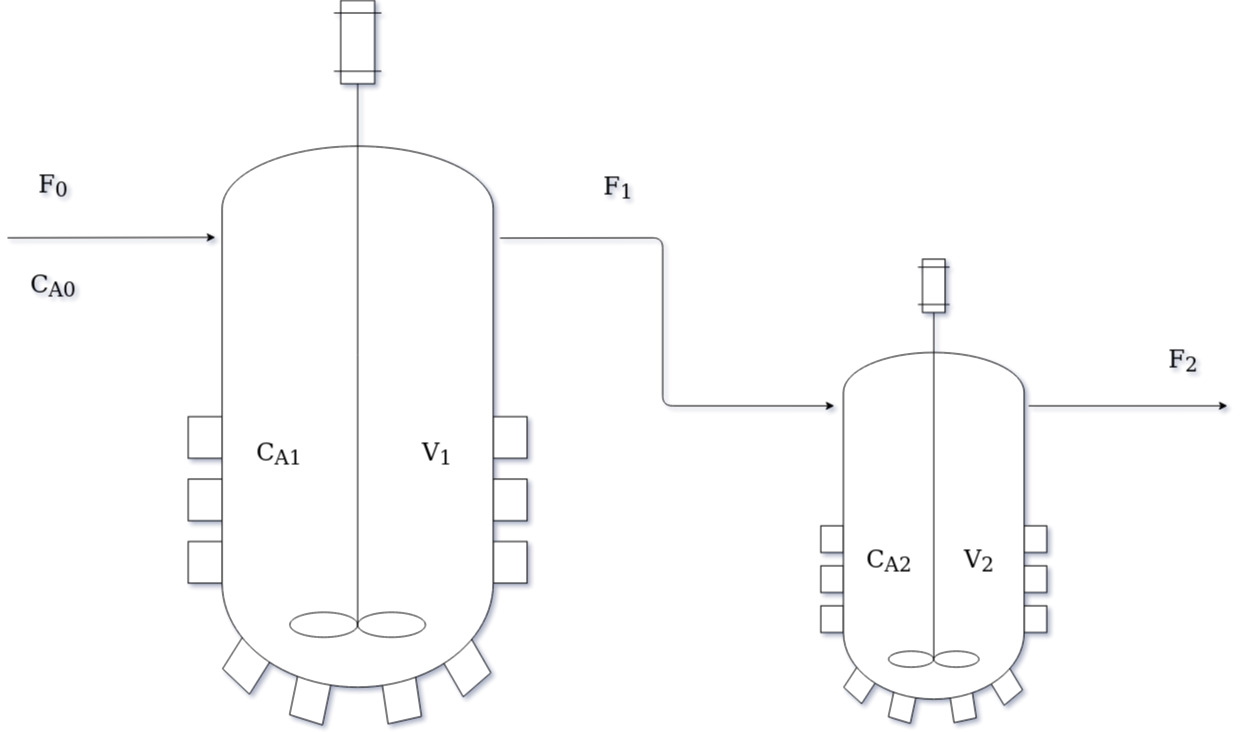
Neste trabalho deseja-se derivar o modelo e sua solução para dois CSTR em série, ilustrados na Figura 1. No tempo t = 0, os dois reatores estão carregados com solvente e catalisador, sem reagente. Ambos são operados a temperatura constante e as densidades são consideradas constantes ao longo dos tanques.
A reação que ocorre é do tipo:
A → B
Com cinética de primeira ordem em relação a A.
Os volumes dos reatores também são constantes pois no início já estão carregados e os produtos são removidos por transbordo. Pode-se assumir também que as vazões $F_0$, $F_1$, e $F_2$ são iguais pois a densidade foi tomada como sempre constante, as saídas ocorrem por transbordo e no momento em que se inicia a análise os tanques estão preenchidos.
Resultados e discussão Link para o cabeçalho
Solução analítica Link para o cabeçalho
Considerações:
-
Os dois reatores são operados a temperatura constante, não serão realizados balanços de energia;
-
As densidades são constantes e independentes das concentrações;
-
Em t = 0 os reatores estão carregados com solvente e catalisador;
-
A reação é: A →B, com cinética de primeira ordem em relação a A e k = 1h$^-$$^1$, de modo que a velocidade de reação é: -r $_A$$_i$ = kC$_A$$_i$;
-
Os volumes dos reatores são constantes (saída por transbordo);
-
Pelas considerações 2, 3 e 5, as vazões $F_0$, $F_1$, e $F_2$ são iguais.
No instante inicial começa-se alimentar o primeiro reator com uma vazão $F_0$ de 2 $m{^3}.h{^-}{^1}$ e concentração constante $C{_A}{_0}$ igual a $300 mol.m{^-}{^3}$. O volume do reator 1 é $10 m{^3}$ e do reator 2, $5 m{^3}$.
Tomando um volume de controle envolvendo o primeiro reator da Figura 1, pode-se escrever o seguinte balanço material:
$$ \frac{d(C_{A1} V_1)}{dt} = F_0 C_{A0} - F_1 C_{A1} + V_1 r_{A1} \tag{1} $$
Como $-r{_A}{_1} = kC{_A}{_1}$, os volumes são constantes e as vazões são todas iguais a $F_0$:
$$ {V{_1}} \frac{d(C{_A}{_1})}{dt} = F_0 C{_A}{_0} - {F_0} C{_A}{_1} - {V_1} k C{_A}{_1} \tag{2} $$
Substituindo os valores conhecidos:
$$ 10m{^3} \frac{d(C{_A}{_1})}{dt} = 2 \frac{m{^3}}{h} 300 \frac{mol}{m³} - 2 \frac{m{^3}}{h} C{_A}{_1} - 10m³ 1h{^-}{^1} C{_A}{_1} \tag{3} $$
Tendo em mente que as unidades utilizadas serão as apresentadas na Equação 3, de agora em diante elas serão omitidas por fins de simplicidade.
Reorganizando a Equação 3:
$$ \frac{5}{ 6 } \frac{ dC{_A}{_1} }{ dt } + C{_A}{_1} = 50 \tag{4} $$
A Equação 4 descreve o comportamento dinâmico do primeiro reator.
Realizando um balanço material em um volume de controle que envolve o segundo reator, temos:
$$ \frac{d(C{_A}{_2} V_2)}{dt} = F_1 C{_A}{_1} - F_2 C{_A}{_2} + V_2 r{_A}{_2} \tag{5} $$
Como $V_2$ é constante, as vazões são todas iguais (consideração 6) e $-r{_A}{_2} = kC{_A}{_2}$:
$$ V_2 \frac{d(C{_A}{_2})}{dt} = F_0 C{_A}{_1} - F_0 C{_A}{_2} - V_2 k C{_A}{_2} \tag{6} $$
Substituindo os valores conhecidos:
$$ 5 \frac{d(C{_A}{_2})}{dt} = 2 C{_A}{_1} - 2 C{_A}{_2} - 5.1.C{_A}{_2} \tag{7} $$
Que pode ser reorganizada como:
$$ \frac{5}{7} \frac{d(C{_A}{_2})}{dt} + C{_A}{_2} = \frac{ 2 }{ 7 } C{_A}{_1} \tag{8} $$
A Equação 8 descreve o comportamento dinâmico do reator dois.
Pode-se partir agora para as soluções analíticas das Equações 4} e 8}. Começando pela Equação 4, uma EDO linear não-homogênea a coeficientes constantes que pode ser resolvida pelo método dos coeficientes a determinar. Sua equação característica é:
$$ \frac{5}{6} \lambda + 1 = 0 \tag{9} $$
Que fornece $\lambda = -1,2$. Com solução homogênea:
$$ C{_A}{_1}{_H} ( t ) = Ce{^{ -1,2t }} \tag{10} $$
A solução particular é uma constante:
$$ C{_A}{_1}{_P} = B \tag{11} $$
Que leva a:
$$ \frac{dC{_A}{_1}{_P}}{ dt } = 0 \tag{12} $$
Aplicando 11} e 12} em 4} encontra-se $B = 50 mol.m{^-}{^3}$.
Portanto,
$$ C{_A}{_1} ( t ) = C{_A}{_1}{_H} + C{_A}{_1}{_P} = Ce{^{ -1,2t }} + 50 \tag{13} $$
Para encontrar $C$ utiliza-se a condição inicial. No tempo $t = 0$ não havia reagente nos tanques ($C{_A}{_1}(0) = 0$), e então $ C = -50 mol.m{^-}{^3}$. A solução da Equação 4 é:
$$ C{_A}{_1} ( t ) = 50 ( 1 - e{^{ -1,2t }} ) \tag{14} $$
A Equação 4 pode ser resolvida também por Laplace, aplicando a transformada:
$$ s C’{_A}{_1} (s) - C{_A}{_1} ( 0 ) + 1,2C’{_A}{_1} ( s ) = \frac{60}{ s } \tag{15} $$
Onde o sinal $(‘)$ é apenas para fazer referência ao domínio de Laplace e diferenciá-lo do domínio do tempo.
Sabendo que $C{_A}{_1}(0)$ é igual a $0$ e simplificando:
$$ C’{_A}{_1} (s) = 50 \frac{ 1 }{ s(\frac{s}{1,2} + 1) } \tag{16} $$
A transformada inversa da Equação 16 nos leva à Equação 14 novamente, confirmando o resultado obtido pelo método dos coeficientes a determinar.
Conhecendo $C{_A}{_1}(t)$ é possível resolver a Equação 8 para o reator 2. Substituindo 14} em 8}:
$$ \frac{5}{7} \frac{d(C{_A}{_2})}{dt} + C{_A}{_2} = \frac{ 100 }{ 7 } - \frac{ 100 }{ 7 } e{^{ -1,2t }} \tag{17} $$
Novamente pelo método dos coeficientes a determinar, a equação característica para a solução homogênea é:
$$ \frac{ 5 }{ 7 } \lambda + 1 = 0 \tag{18} $$
Que leva a $\lambda = -1,4$. E à solução homogênea:
$$ C{_A}{_2}{_H} ( t ) = C{_1} e{^{ -1,4t }} \tag{19} $$
A equação particular é da forma:
$$ C{_A}{_2}{_P} ( t ) = A -B e{^{ -1,2t }} \tag{20} $$
Derivando 20}:
$$ \frac{ d(C{_A}{_2}{_P})}{ dt } = 1,2 B e{^{ -1,2t }} \tag{21} $$
Aplicando 20} e 21} em 17} e agrupando os termos:
$$ A - \frac{ B }{ 7 } e{^{ -1,2t }} = \frac{ 100 }{ 7 } - \frac{ 100 }{ 7 } e{^{ -1,2t }} \tag{22} $$
Portanto, comparando os dois lados da Equação 22 percebe-se que $A = \frac{100}{7} mol.m{^-}{^3}$ e $B = 100 mol.m{^-}{^3}$. Isso leva a:
$$ C{_A}{_2}{_P} ( t ) = \frac{100}{7} -100 e{^{ -1,2t }} \tag{23} $$
E a solução da Equação 8 é, portanto:
$$ C{_A}{_2} ( t ) = C{_A}{_2}{_H} + C{_A}{_2}{_P} = C_1 e{^{ -1,4t }} - 100 e{^{ -1,2t }} + \frac{ 100 }{ 7 } \tag{24} $$
Como a condição inicial é $C{_A}{_2}(0) = 0$, encontra-se $C{_1} = \frac{600}{7} mol.m{^-}{^3}$. Substituindo $C{_1}$ na Equação 24:
$$ C{_A}{_2} ( t ) = \frac{600}{7} e{^{ -1,4t }} - 100 e{^{ -1,2t }} + \frac{ 100 }{ 7 } \tag{25} $$
A Equação 25 é a solução analítica da Equação 8, que pode ser resolvida também aplicando as transformadas de Laplace termo a termo:
$$ 0,71429 [ {sC’{_A}{_2} (s) - C{_A}{_2} (0)} ] + C’{_A}{_2} ( s ) = \frac{ 14,286 }{ s } - 14,286 \frac{ 1 }{ s+1,2 } \tag{26} $$
Rearranjando 26}:
$$ C’{_A}{_2} (s) = \frac{ 14,286 }{ s(0,71429s + 1) } - 11,905 \frac{ 1 }{ (\frac{s}{1,2} + 1) (0,71429s+1)} \tag{27} $$
A transformada inversa da Equação 27 é:
$$ C{_A}{_2} ( t ) = 14,286 ( 1 - e{^{-1,4t}} ) - 11,905 \frac{1}{\frac{1}{1,2} - 0,71429} ( e{^{-1,2t}} - e{^{-1,4t}} ) \tag{28} $$
Rearranjando:
$$ C{_A}{_2} ( t ) = 85,714 e{^{ -1,4t }} - 100 e{^{ -1,2t }} + 14,286 \tag{29} $$
Observando que $\frac{600}{7} ≈ 85,714$ e $\frac{100}{7} ≈ 14,286$, chegamos novamente à Equação 25, confirmando nossa solução.
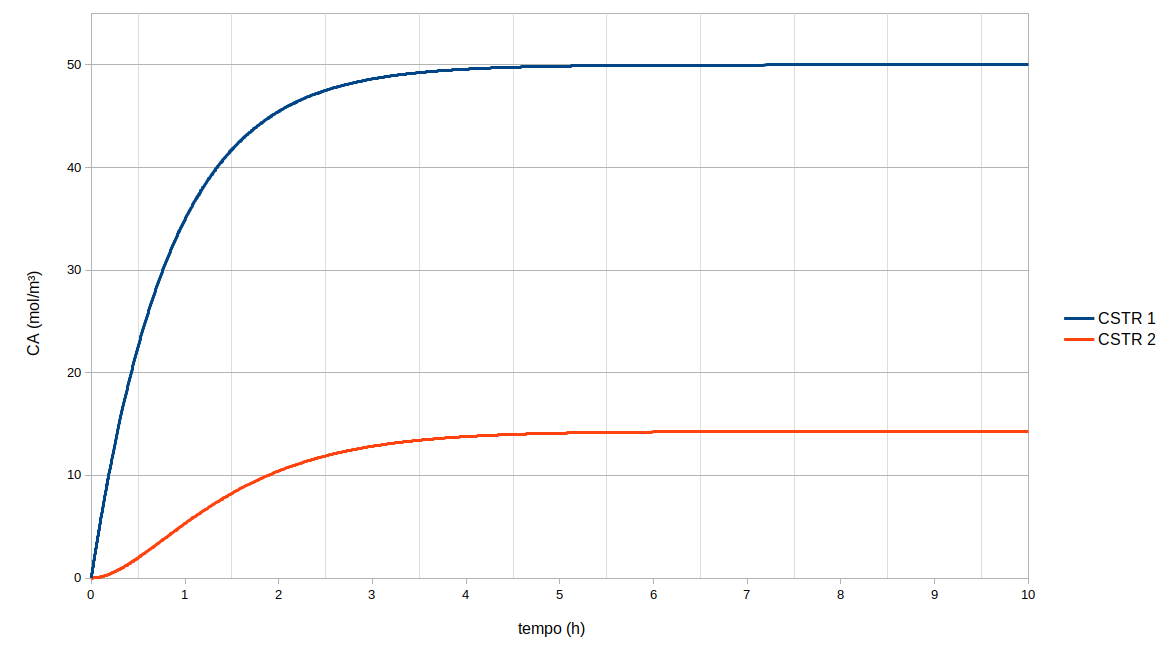
Com as soluções prontas pode-se traçar um gráfico com os comportamentos das concentrações em cada reator, na Figura 2 pode-se observar que a concentração no CSTR 1 é sempre maior que no segundo, como é de se esperar, pois o reator 1 é alimentado primeiro e parte do reagente é consumido antes que se alimente o reator 2.
Percebe-se também que ambos os CSTRs atingem o regime permanente aproximadamente no mesmo tempo, em torno de 5 horas, com concentrações $C{_A}{_1} = 50 mol.m{^-}{^3}$ e $C{_A}{_2} = 14,285 mol.m{^-}{^3}$.
As conversões, o que reage pelo que é alimentado, podem ser calculadas como:
$$ X{_1} = \frac{V{_1}kC{_A}{_1}}{ F_0 C{_A}{_0} } \tag{30} $$
$$ X{ _2 } = X{_1} + \frac{V{ _2 }kC{_A}{_2}}{ F_0 C{_A}{_0} } \tag{31} $$
Ambas definidas com relação à alimentação $F_0$.
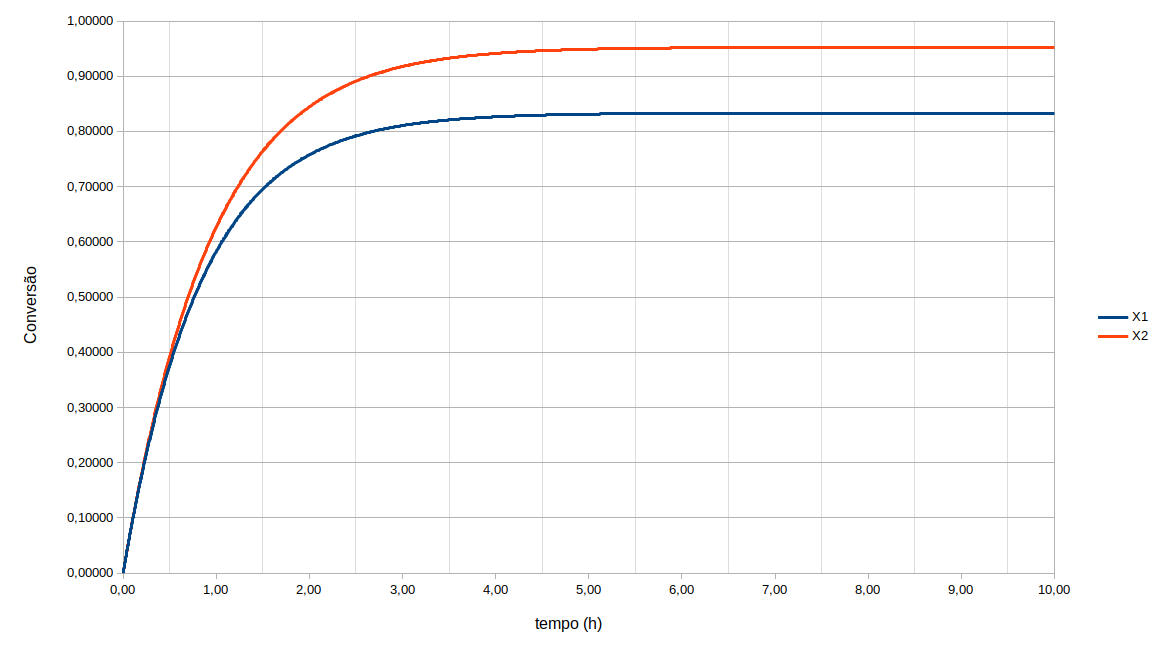
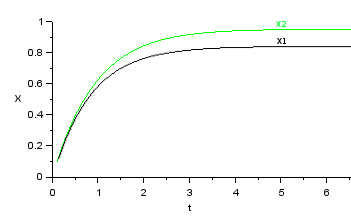
As Equações 30} e 31} nos levam, no estado estacionário, a um $X_1$ intermediário de $0,8333$ e uma conversão final $X_2$ igual a $0,9524$.
Pode-se traçar também um gráfico relacionando o tempo com a conversão, como na Figura 3. Observa-se que no início as duas conversões são muito próximas, isto é consequência da definição adotada, que é sempre em relação à alimentação original. No primeiro instante o termo de consumo no reator dois é nulo e a conversão final é igual à intermediária. Conforme o tempo aumenta, reagente passa a entrar no segundo reator e o termo da conversão final começa a se distanciar da conversão intermediária.
Solução Numérica Link para o cabeçalho
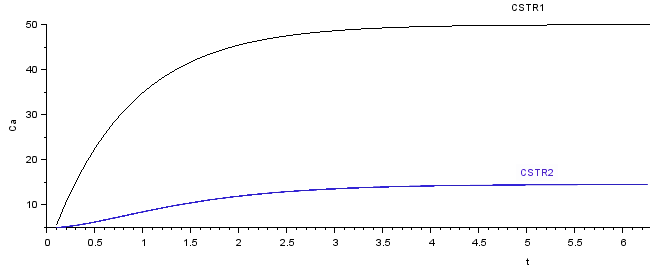
Utilizando-se do método de Runge-Kutta de quarta ordem (RK45) para resolução do modelo criado no Xcos (Figura 6) foram obtidos perfis de concentração do componente A, e conversão intermediaria $X_1$ e final $X_2$ como segue.
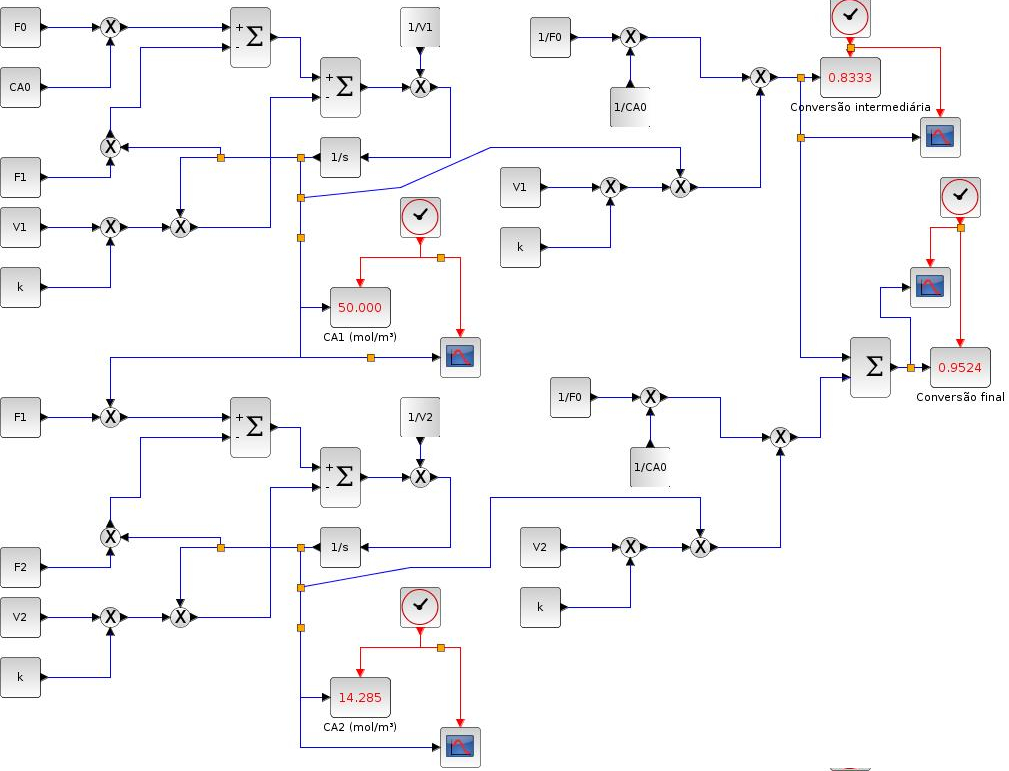
Baixe o arquivo da Figura 6 aqui
Qualitativamente observa-se que as curvas acima de concentração de A e de conversão em função do tempo obtidas na solução numérica apresentam as mesmas características das curvas obtidas analiticamente (apresentadas nas Figuras 2 e 3).
Em estado estacionário a solução numérica resulta em $C{_A}{_1} = 50 mol.m{^-}{^3}$ $C{_A}{_2} = 14,286 mol.m{^-}{^3}$.
Para comparação dos dados obtidos numericamente partimos da analise de estado estacionário do modelo desenvolvido como segue:
Da Equação 4: $\frac{5}{ 6 } \frac{ dC{_A}{_1} }{ dt } + C{_A}{_1} = 50$, em estado estacionário temos:
$$ \frac{ dC{_A}{_1} }{ dt } = 0 $$
Então: $\frac{5}{ 6 } 0 + {\bar C}{_A}{_1} = 50$, que leva a ${\bar C}{_A}{_1} = 50$.
Da equação 8: $\frac{5}{7}\frac{d(C{_A}{_2})}{dt} + C{_A}{_2} = \frac{ 2 }{ 7 } C{_A}{_1}$ e da consideração de estado estacionário:
$$ \frac{d(C{_A}{_2})}{dt} = 0 $$
Portanto:
$$ {\bar C}{_A}{_2} = \frac{ 2 }{ 7 } 50 = \frac{100}{7} $$
Temos portanto ${\bar C}{_A}{_2} \approx 14.286 { mol }{ m{^-}{^3} }$ valor que difere em $0.001$ do valor obtido numericamente, enquanto o valor de ${\bar C}{_A}{_1} = 50{ mol }.m{^-}{^3}$ é exatamente o mesmo obtido numericamente.
O esquema numérico utilizado se mostra como uma boa alternativa aos métodos analíticos, apresentando valores muito próximos destes com reduzida complexidade na obtenção dos resultados.
Alterando os volumes dos reatores da simulação observou-se que dois reatores de igual volume resultam numa conversão ligeiramente maior, como pode ser observado na Tabela 1. Isso se deve ao fato de que a utilização de CSTRs de mesmo volume arranjados em série aproxima o comportamento de um PFR, o qual apresenta conversão mais alta para um mesmo volume em reações de primeira ordem.
Observa-se ainda que não há efeito na conversão final ao se inverter a ordem do reator maior e o menor de forma que do ponto de vista da obtenção do produto não faz diferença a ordem dos reatores.
Tabela 1 - Concentrações e conversões em diferentes volumes.
| V1 e V2 | Conversão Intermediária | Concentração no Primeiro Reator | Conversão Final | Concentração no Segundo Reator |
|---|---|---|---|---|
| 5 e 10 m³ | 0.7143 | 85.714 mol/m³ | 0.9524 | 14,285 mol/m³ |
| 10 e 5 m³ | 0.8333 | 50 mol/m³ | 0.9524 | 14.285 mol/m³ |
| 7.5 e 7.5 m³ | 0.7895 | 63 mol/m³ | 0.9557 | 13.296 mol/m³ |