Operação de Reator Não-Adiabático: Oxidação do Dióxido de Enxofre

Introdução Link para o cabeçalho

O trióxido de enxofre é utilizado na fabricação do ácido sulfúrico partindo da queima do enxofre, seguida da oxidação do dióxido de enxofre produzido na primeira reação ¹. O ácido sulfúrico é o produto químico de maior volume de produção nos Estados Unidos e um ótimo indicador do grau de industrialização de um país ². O enxofre pode ser obtido de depósitos de minério, ou a partir da extração de sulfeto de hidrogênio do gás natural e petróleo ².

Em 2020, o Brasil produziu 500 mil toneladas de ácido sulfúrico ³. Os maiores produtores foram China, Estados Unidos e Rússia, com 17 milhões, 8,1 milhões e 7,5 milhões de toneladas respectivamente ³.

O maior consumidor de ácido sulfúrico é a indústria de fertilizantes, na obtenção de ácido fosfórico para produção de fertilizantes fosforados ⁴, em torno de metade da produção mundial é direcionada para este ramo ⁵. Outros usos incluem baterias, produtos de limpeza, na indústria metalúgica para limpeza e prevenção de corrosão prévia a processos de revestimento, como matéria prima para produção de outros ácidos, como o clorídrico, fosfórico e nítrico, na produção de papel e no refino de petróleo ⁵.

Resultados e discussão Link para o cabeçalho

A reação de interesse deste trabalho é a oxidação do $SO_2$:

$$ SO_2 + \frac{ 1 }{ 2 } O_2 + Inerte ⇌ SO_3 + Inerte \tag{1} $$

Para simplificar a notação chamaremos o $SO_2$, $O_2$ e $SO_3$ de $A$, $B$ e $C$, nesta ordem.

$$ A + \frac{ 1 }{ 2 } B + I ⇌ C + I \tag{2} $$

Sua lei de velocidade foi estudada por Eklund e apresentada por Fogler ¹ em seu livro texto:

$$ -{r_A}’ = k \sqrt{ \frac{P_A}{P_C} } \left [ P_B - \left ( \frac{ P_C }{K_P P_A} \right )^2 \right ] \tag{3} $$

A lei de velocidade da Equação 3 é válida entre 1278 ºR e 1489 ºR, e pode ser utilizada quando a conversão é maior que 5%; a conversões menores que 5% a lei de velocidade é aquela para a conversão de 5%. Os parâmetros $k$ e $K_p$ são a velocidade específica de reação e a constante de equilíbrio, dados abaixo, onde $T$ é a temperatura e $R$ a constante dos gases ideais ($1,987 Btu.lbmol^{-1}.^{o}R^{-1}$).

$$ k = exp \left [ \frac{-176 008}{T} - 110,1 ln(T) + 912,8 \right ] \tag{4} $$

$$ K_p = exp \left [ \frac{42 311}{RT} - 11,24 \right ] \tag{5} $$

O catalisador foi utilizado na forma de pellets de $8 mm$ de diâmetro e $8 mm$ de comprimento, em um leito de massa específica $33,8 lb.ft^{-3}$.

O reator a ser utilizado é um conjunto de tubos de leito fixo paralelos, resfriados por um líquido em ebulição. O coeficiente global de transferência de calor ($U$) é igual a $10 Btu.h^{-1}.ft^{-2}$. A velocidade mássica de alimentação é $75 ft^{3}.min^{-1}.ft^{-2}$.

Fogler ¹ parte de dados de conversão em reatores adiabáticos, para definir um volume total de catalisador de $3910 ft^{3}$. Nos reatores adiabáticos este volume leva a uma conversão de 88 %.

Foram selecionados tubos de diâmetro externo $3 in$ e diâmetro interno $2,782 in$, com $20 ft$ de comprimento. Calculando o número de tubos:

$$ N_{tubos} = \frac{3910 ft^3}{ \pi {\left ( \frac{2,782 i n \frac{1ft}{12 i n}} {2} \right )}^2 20 ft } = 4632 tubos \tag{6} $$

Obtêm-se $4632$ tubos. Assim, a área de seção transversal total ($A_{CT}$) é:

$$ A_{CT} = { \pi {\left ( \frac{2,782 in \frac{1ft}{12 i n}}{2} \right )}^2 } 4632 tubos = 195,53 ft^2 \tag{7} $$

Conhecendo a velocidade mássica e área de seção transversal obtém-se a vazão de alimentação ($v_0$):

$$ v_0 = 75 \frac{ ft^3 }{ min . ft^2 } 195,53 ft^2 = 14664,75 \frac{ ft^3 }{ min } \tag{8} $$

A alimentação é dada como $7900 lbmol.h^{-1}$, à pressão inicial de $2 atm$ e frações molares de $0,11$ para o $SO_{2}$, $0,10$ para o $O_{2}$ e $0,79$ para o $N_{2}$. O reator opera em regime permanente e um resumo dos parâmetros é apresentado na Tabela 1.

Tabela 1: Parâmetros

Parâmetro	Símbolo	Valor	Unidade
Porosidade do leito	$\phi$	0,45	$Adimensional$
Densidade da alimentação	$\rho_{0}$	0,054	$lb.ft^{-3}$
Pressão inicial	$P_0$	2	$atm$
Diâmetro das partículas de catalisador	$D_p$	0,015	$ft$
Viscosidade	$\mu$	0,090	$lb.ft^{-1}.h^{-1}$
Coeficiente global de transferência de calor	$U$	10	$Btu.h^{-1}.ft^{-2}.^{o}R^{-1}$
Área de seção transversal de um tubo	$A_C$	0,0422	$ft^2$
Fator de conversão força-massa	$g_c$	4,17E8	$lbm.ft.lbf^{-1}.h^{-2}$
Densidade do leito	$\rho_b$	33,8	$lb.ft^{-3}$

Balanço de Massa Link para o cabeçalho

Os balanços serão realizados para um único tubo, pois eles estão em paralelo, então os perfis de conversão, pressão e temperatura são iguais em todos. O balanço de massa em um reator tubular de leito empacotado é realizado observando a Figura 1.

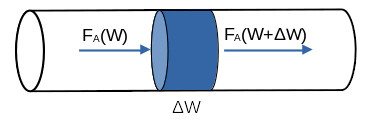
Tomando uma quantidade de catalisador $\Delta W$ do reator e aplicando o balanço de massa em regime permanente:

$$ F_A ( W ) - F_A ( W + \Delta W) + {r_A}’ \Delta W = 0 \tag{9} $$

Dividindo a Equação 6 por $\Delta W$ e tomando o limite quando $\Delta W$ tende a zero, chegamos a:

$$ -{\frac{ dF_A }{ dW }} = -{ r_A }' \tag{10} $$

Construindo a Tabela Estequiométrica (Tabela 2):

Tabela 2: Tabela Estequiométrica.

Espécie	Entrada	Variação	Saída
$ A $	$ F_{A0} $	$ -F_{A0}X $	$ F_{A} = F_{A0}(1-X) = F_{A0} (θ_A + ν_AX) $
$ B $	$ F_{B0} = 0,91 F_{A0} = θ_AF_{A0} $	$ -0,5F_{A0}X $	$ F_{B} = F_{A0}(0,91 – 0,5X) = F_{A0} (θ_B + ν_BX) $
$ C $	$ F_{C0} = 0 = θ_C F_{A0} $	$ F_{A0}X $	$ F_{C} = F_{A0}X = F_{A0} (θ_C + ν_BX) $
$ I $	$ F_{I0} = 7,18F_{A0} = θ_AF_{A0} $	$ 0 $	$ F_I = F_{I0} = F_{A0} (θ_I + ν_IX) $
Total	$ F_{T0} = 9,09F_{A0} $	$ -0,5F_{A0}X $	$ F_T = F_{T0} – 0,5F_{A0}X = F_{A0}(9,09 – 0,5X) $

Escrevendo as concentrações em função da conversão (X):

$$ C_A = \frac{ F_A }{ v } \tag{11} $$

Da lei dos gases ideais extrai-se a vazão volumétrica ($v$):

$$ v = v_0 \frac{ F_T T P_0 }{ F_{T0} T_0 P } \tag{12} $$

Da Tabela 2 encontra-se que $F_T/F_{T0}$ é:

$$ \frac{ F_T }{ F_{T0} } = 1 - 0,5 y_{ A0 }X = 1-0,055X \tag{13} $$

Substituindo a Equação 13 na 12:

$$ v = v_0 { (1 - 0,055X) } \frac{ T }{ T_0 } \frac{ P_0 }{ P } \tag{14} $$

Inserindo a Equação 14 na 11, utilizando a Tabela 2 para abrir $F_A$ e sabendo da lei dos gases ideais que $C_A = P_A/(RT)$:

$$ P_A = P_{A0} \frac{ (1-X) }{ (1-0,055X) } \frac{ P }{ P_0 } \tag{15} $$

Da mesma forma encontram-se as pressões parciais para $B$, $C$ e $I$:

$$ P_B = P_{A0} \frac{ (0,91-0,5X) }{ (1-0,055X) } \frac{ P }{ P_0 } \tag{16} $$

$$ P_C = P_{A0} \frac{ X }{ (1-0,055X) } \frac{ P }{ P_0 } \tag{17} $$

$$ P_I = P_{A0} \frac{ 7,18 }{ (1-0,055X) } \frac{ P }{ P_0 } \tag{18} $$

Aplicando as Equações 15 a 18 na Equação 3, com $P_{A0} = 0,22 atm$, obtém-se a velocidade de reação em função da conversão, temperatura e pressão:

$$ -{ r_A }’ = k \sqrt{ \frac{1-X}{X} } \left [ \frac{ (0,20 - 0,11X) }{(1-0,055X)} \frac{P}{P_0} - \left ( \frac{ X }{K_p (1-X)} \right ) ^2 \right ] \tag{19} $$

Substituindo a Equação 19 no balanço de massa (Equação 10) e observando da Tabela 2 que $dF_A = -F_{A0}dX$ e $F_{A0} {\frac{ dX }{ dW }} = -{ r_A }’$. Aparece a equação diferencial ordinária do balanço de massa:

$$ \frac{dX}{ dW } = \frac{ k }{ F_{A0} } \sqrt{ \frac{1-X}{X} } \left [ \frac{ (0,20 - 0,11X) }{(1-0,055X)} \frac{P}{P_0} - \left ( \frac{ X }{K_p (1-X)} \right ) ^2 \right ] \tag{20} $$

A alimentação de $A$ ($F_{A0}$) é:

$$ F_{A0} = \frac{7900 \frac{ lbmol }{ h } 0,11}{ 4632 tubos } = 0,188 \frac{ lbmol }{ h.tubo } \tag{21} $$

Balanço de Energia Link para o cabeçalho

Agora, do balanço de energia para um sistema aberto temos:

taxa de acúmulo de energia	=	taxa de entrada de energia através de massa que entra no sistema	-	taxa de saída de energia através da massa que sai do sistema	+	taxa de transferência de calor das vizinhanças para o sistema	-	taxa de variação do trabalho realizado pelo sistema sobre as vizinhanças

Portanto, no regime permanente e sem taxa de trabalho:

$$ F_{entra} E_{entra} - F_{sai} E_{sai} + \dot{ Q } - \dot{W} = 0 \tag{22} $$

Onde $F$ são vazões molares, $E$ taxa de energia, $\dot{Q}$ e $\dot{W}$ taxas de calor e trabalho. Escrevendo a Equação 22 em termos das $n$ espécies:

$$ {\sum_{i=1}^{n} E_{i0} F_{i0}} - { \sum_{i=1}^{n} E_i F_i } + \dot{Q} - \dot{W} = 0 \tag{23} $$

Neste caso, a única contribuição do termo de trabalho é o trabalho de escoamento:

$$ -\dot{W} = { \sum_{i=1}^{n} F_{i0} P V_{i0}} - { \sum_{i=1}^{n} F_i P V_i } \tag{24} $$

Substituindo a Equação 24 na 23 e agrupando os termos:

$$ { \sum_{i=1}^{n} F_{i0} (E_{i0} + P V_{i0}) } - { \sum_{i=1}^{n} F_i (E_i + PV_i) } + \dot{Q} = 0 \tag{25} $$

O termo de energia ($E_i$) é composto pelas energias interna, cinética e potencial:

$$ E_i = U_i + \frac{ 1 }{ 2 } {u_i}^2 + gz_i \tag{26} $$

O reator é fixo no espaço e sua altura é de apenas $20 ft$, portanto é possível desprezar as variações nas energias cinética e potencial:

$$ E_i = U_i \tag{27} $$

Então a Equação 25 fica:

$$ { \sum_{i=1}^{n} F_{i0} (U_{i0} + P V_{i0}) } - { \sum_{i=1}^{n} F_i (U_i + PV_i) } + \dot{Q} = 0 \tag{28} $$

Sabemos que o termo $U + PV$ é chamado, por conveniência, de entalpia ($H$):

$$ { \sum_{i=1}^{n} F_{i0} H_{i0} } - { \sum_{i=1}^{n} F_i H_i } + \dot{Q} = 0 \tag{29} $$

Desdobrando as somatórias da Equação 29, para nossas espécies $A$, $B$, $C$ e $I$ (da Tabela 2):

$$ { \sum_{i=1}^{n} F_{i0} H_{i0} } - { \sum_{i=1}^{n} F_i H_i } = ( H_{A0} F_{A0} + H_{B0} F_{B0} + H_{i0} F_{i0} ) - ( F_A H_A + F_B H_B + F_C H_C + F_I H_I ) \tag{30} $$

Em termos da conversão:

$$ { \sum_{i=1}^{n} F_{i0} H_{i0} } - { \sum_{i=1}^{n} F_i H_i } = F_{A0} [ H_{A0} + \theta_B H_{B0} + \theta_i H_{i0} - H_A - \theta_B H_B + \theta_i H_i] - F_{A0} X ( -H_A - \frac{1}{2} H_B + H_C ) \tag{31} $$

O termo $( -H_A - \frac{1}{2} H_B + H_C )$ da Equação acima é a entalpia de reação ($\Delta H_{RX}$), inserindo-a na Equação 31 e agrupando os termos:

$$ { \sum_{i=1}^{n} F_{i0} H_{i0} } - { \sum_{i=1}^{n} F_i H_i } = F_{A0} {\sum_{i=1}^{n} \theta_i (H_{i0} - H_i)} - F_{A0} X \Delta H_{RX} \tag{32} $$

Substituindo a Equação 32 na 29:

$$ \dot{Q} + F_{A0} {\sum_{i=1}^{n} \theta_i (H_{i0} - H_i)} - F_{A0} X \Delta H_{RX} = 0 \tag{33} $$

A taxa de calor ($\dot{Q}$) vem da lei do resfriamento de Newton.

$$ \dot{Q} = UA ( T_a - T ) \tag{34} $$

Onde $A$ é a área de troca térmica ($2 \pi r L = 14,567 ft^2$), e $T_a$ a temperatura do líquido de troca térmica ($1264,67 ^oR$).

As entalpias estão relacionadas com a entalpia de formação a uma temperatura de referência ($T_R$), para um sistema sem mudança de fase, da seguinte forma:

$$ H_i = { H_i }^o ( T_R ) + \int_{ T_R }^{ T } C_{pi} dT \tag{35} $$

As capacidades caloríficas ($C_{pi}$) são polinômios de grau dois:

$$ C_{pi} = \alpha_i + \beta_i T + \gamma_i T^2 \tag{36} $$

As constantes da Equação 36 são listadas na Tabela 3.

Tabela 3: Constantes das capacidades caloríficas.

Espécie	$\alpha_i (btu.lbmol^{-1}.^oR^{-1})$	$\beta_i (btu.lbmol^{-1}.^oR^{-2})$	$\gamma_i (btu.lbmol^{-1}.^oR^{-3})$
$ A $	7,208	5,633E-3	-1,343E-6
$ B $	5,731	2,323E-3	-4,886E-7
$ C $	8,511	9,517E-3	-2,325E-6
$ I $	6,248	8,778E-4	-2,13E-8

Escrevendo $H_{i0} – Hi$ a partir da Equação 35:

$$ H_{i0} - H_i = { H_i }^o ( T_R ) + { \int_{T_R}^{T_{i0}} C_{pi} dT } - { H_i }^o( T_R ) + { \int_{T}^{T_R} C_{pi} dT } = - { \int_{T_{i0}}^{T} C_{pi} dT} \tag{37} $$

Substituindo a Equação 37 na 33:

$$ \dot{Q} - F_{A0} {\sum_{i=1}^{n} { \int_{T_i0}^{T} \theta_i C_{pi} dT}} - F_{A0} X \Delta H_{RX} = 0 \tag{38} $$

Substituindo o termo de entalpia de reação com a Equação 35:

$$ \Delta H_{RX} ( T ) = { H_C }^o + \int_{ T_R }^{ T } C_{pC} dT - \frac{1}{2}{ H_B }^o -\frac{1}{2} \int_{ T_R }^{ T } C_{pB} dT - { H_A }^o + \int_{ T_R }^{ T } C_{pA} dT $$

$$ \Delta H_{RX} ( T ) = { H_C }^o - \frac{1}{2}{ H_B }^o - { H_A }^o + \int_{ T_R }^{ T } ( C_{pC} - \frac{1}{2} C_{pB} - C_{pA} ) dT = \Delta H_{RX} ^o( T_R ) + \int_{ T_R }^{ T } \Delta C_p dT \tag{39} $$

A entalpia de reação para a temperatura de referência de $1260 ^oR$ é $-42 471 btu.lbmol de A^{-1}$. Da Equação 36 e Tabela 3 encontra-se o seguinte $\Delta C_p$:

$$ \Delta C_p = -1,5625 + 2,7225 * 10^{-3}T - 7,377 * 10^{-7} T^2 \tag{40} $$

E a entalpia de reação fica:

$$ \Delta H_{RX} ( T ) = -42471 - 1,5625( T-1260 ) + 1,36*10^{-3} ( T^2 -1260^2 ) - 2,459*10^{-7} ( T^3 - 1260^3 ) \tag{41} $$

Diferenciando o balanço de energia (Equação 38) em relação à quantidade de catalisador ($W$), e observando que no último termo deve-se utilizar a regra da cadeia pois $X\Delta H_{RX} = f( T, X )$:

$$ \frac{d \dot{Q}}{ dW } - F_{A0} { \sum_{i=1}^{n} \theta_i C_{pi}} \frac{ dT }{ dW } - \Delta H_{RX} F_{A0} \frac{ dX }{ dW } - F_{A0} X \Delta C_p \frac{ dT }{ dW } - F_{A0} \frac{ dX }{ dW } { \int_{T_R}^{T} \Delta C_p dT} = 0 \tag{42} $$

Para encontrar a derivada da taxa de troca de calor em relação à quantidade de catalisador utilizamos a razão entre área de troca térmica e volume de leito ($a = A_{troca}/V_{leito} = 4/D$) e substituímos na Equação 34:

$$ \dot{Q} = U{\frac{4}{D}}V_{leito}( T_a - T ) \tag{43} $$

Pode-se relacionar o volume de leito com a quantidade de catalisador da seguinte forma:

$$ V_{leito} = \frac{ W }{ \rho_b } \tag{44} $$

Substituindo 44} em 43} e diferenciando em relação a $W$:

$$ \frac{d \dot{Q}}{ dW } = \frac{ 4U }{ \rho_b D } ( T_a -T ) \tag{45} $$

Substituindo $\frac{ dX }{ dW }$ por $-r_A’$ e $\frac{d \dot{Q}}{dW}$ na Equação 42:

$$ \frac{ 4U }{ \rho_b D } ( T_a -T ) - F_{A0}({ \sum_{i=1}^{n} \theta_i C_{pi}} )\frac{ dT }{ dW } - F_{A0} ( \Delta H_{RX}^o + \int_{T_R}^T \Delta C_p dT) \frac{ -r_A’}{ F_{A0} } = 0 \tag{46} $$

Rearranjando e simplificando, chegamos à EDO do balanço de energia:

$$ \frac{dT}{ dW } = \frac{\frac{ 4U }{ \rho_b D } ( T_a -T ) + ( -r_A’ )( - \Delta H_{RX} )}{ F_{A0} ( \sum_{i=1}^{n} \theta_i C_{pi} + X \Delta C_p)} \tag{47} $$

Balanço de Momento Link para o cabeçalho

Para a perda de pressão utilizamos a Equação de Ergun:

$$ \frac{ dP }{ dz } = - \frac{ G }{ \rho g_c D_p } \frac{ 1 - \phi }{ \phi ^3 } \left [ \frac{ 150 (1 - \phi) }{D_p} + 1,75G \right ] \tag{48} $$

Em que:

$P$ é a pressão;

$z$ o comprimento ao longo do leito;

$g_c$ o fator de conversão força-massa;

$\phi$ a porosidade do leito;

$D_p$ o diâmetro de partícula;

$\rho$ a densidade do fluido e;

$G$ a velocidade Mássica.

Substituindo a massa de catalisador em função de $z$ ($dz = \frac{4dW}{\rho_b \pi { D^2 }}$), e a densidade da lei dos gases ideais ($\rho = \rho_0 \frac{ P }{ P_0 } \frac{ T_0 }{ T } ( 1-0,055X )$) na Equação 48:

$$ \frac{ dP }{ dW } = -\frac{4}{\rho_b \pi D^2} \frac{ G (1-0,055X) }{ g_c D_p \rho_0 } \frac{P_0}{P} \frac{T}{T_0} \frac{ 1 - \phi }{ \phi ^3 } \left [ \frac{ 150 (1 - \phi) } {D_p} + 1,75G \right ] \tag{49} $$

Solução Numérica do Sistema de Equações Diferenciais e Discussão dos Resultados Link para o cabeçalho

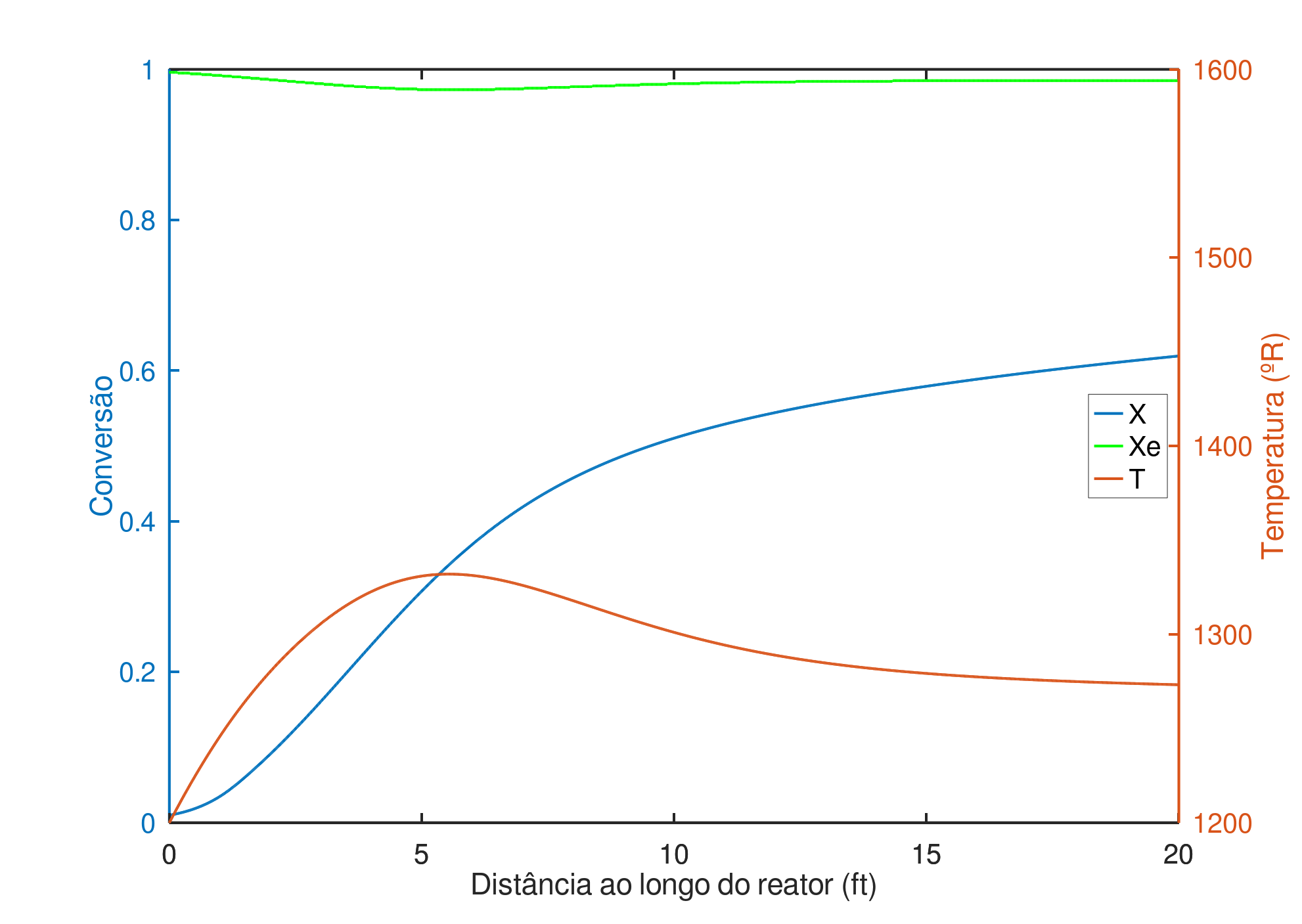
Resolvendo numericamente o sistema de equações diferenciais 20}, 47} e 49} no software Octave versão 6.2.0, utilizando o método de Dormand-Prince de ordem 4, com pressão inicial de $2 atm$, conversão inicial zero e temperatura na entrada de $1200 ^oR$, obtemos o gráfico da Figura 2, com as curvas de temperatura, conversão e conversão de equilíbrio (quando a velocidade de reação é nula).

Link para os códigos do Octave

Percebe-se da Figura 2 que a conversão está muito abaixo da conversão de equilíbrio devido à baixa temperatura de alimentação, outro ponto a se notar é que a temperatura do fluido de refrigeração é mais alta que a temperatura de entrada, de maneira que nos primeiros $1,5 ft$ do reator, o fluido de refrigeração na verdade fornece calor para o reator, a partir desse ponto a temperatura aumenta até um máximo de $1332 ^oR$ caindo a $1273 ^oR$ na saída, com conversão final de 62%.

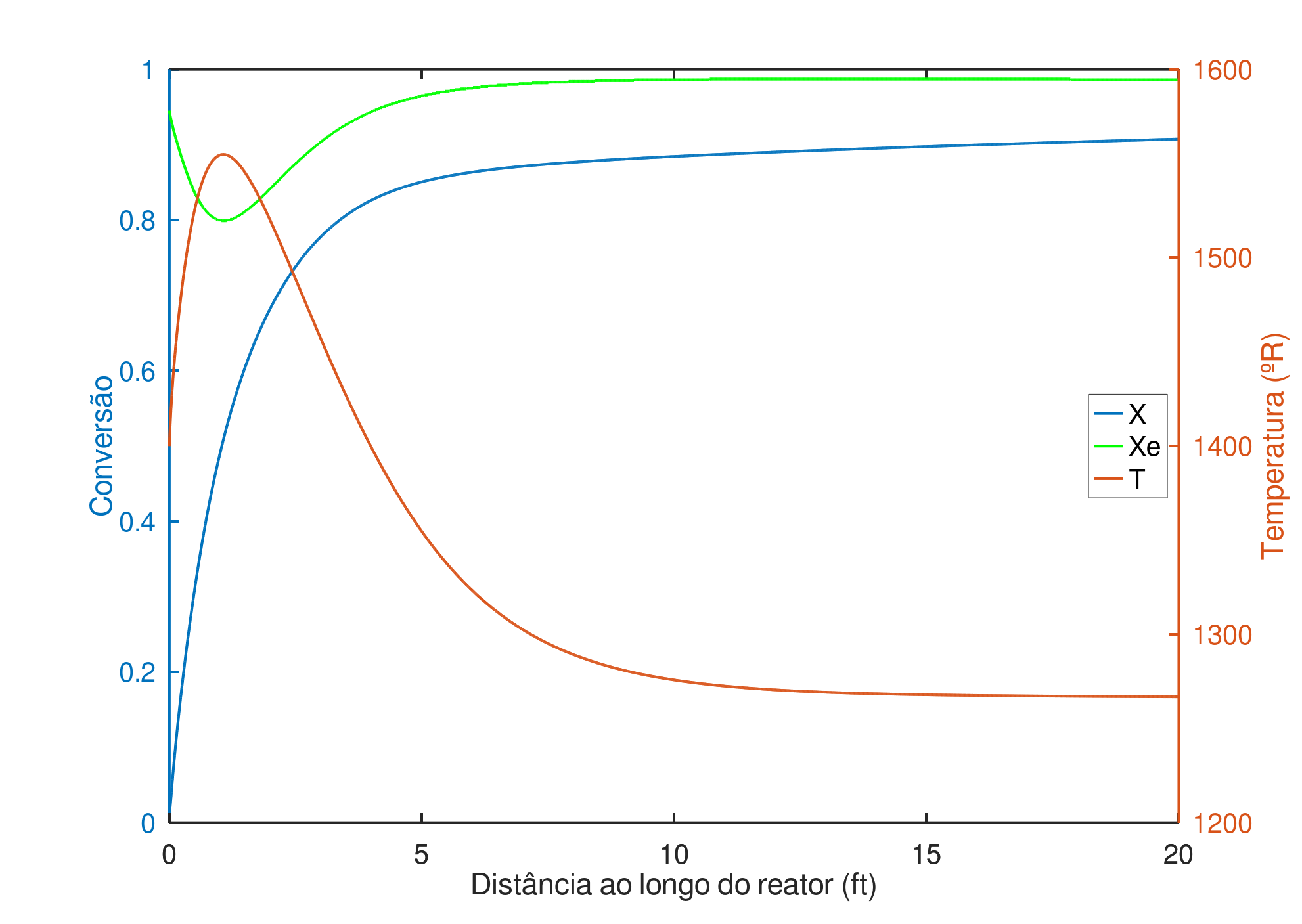
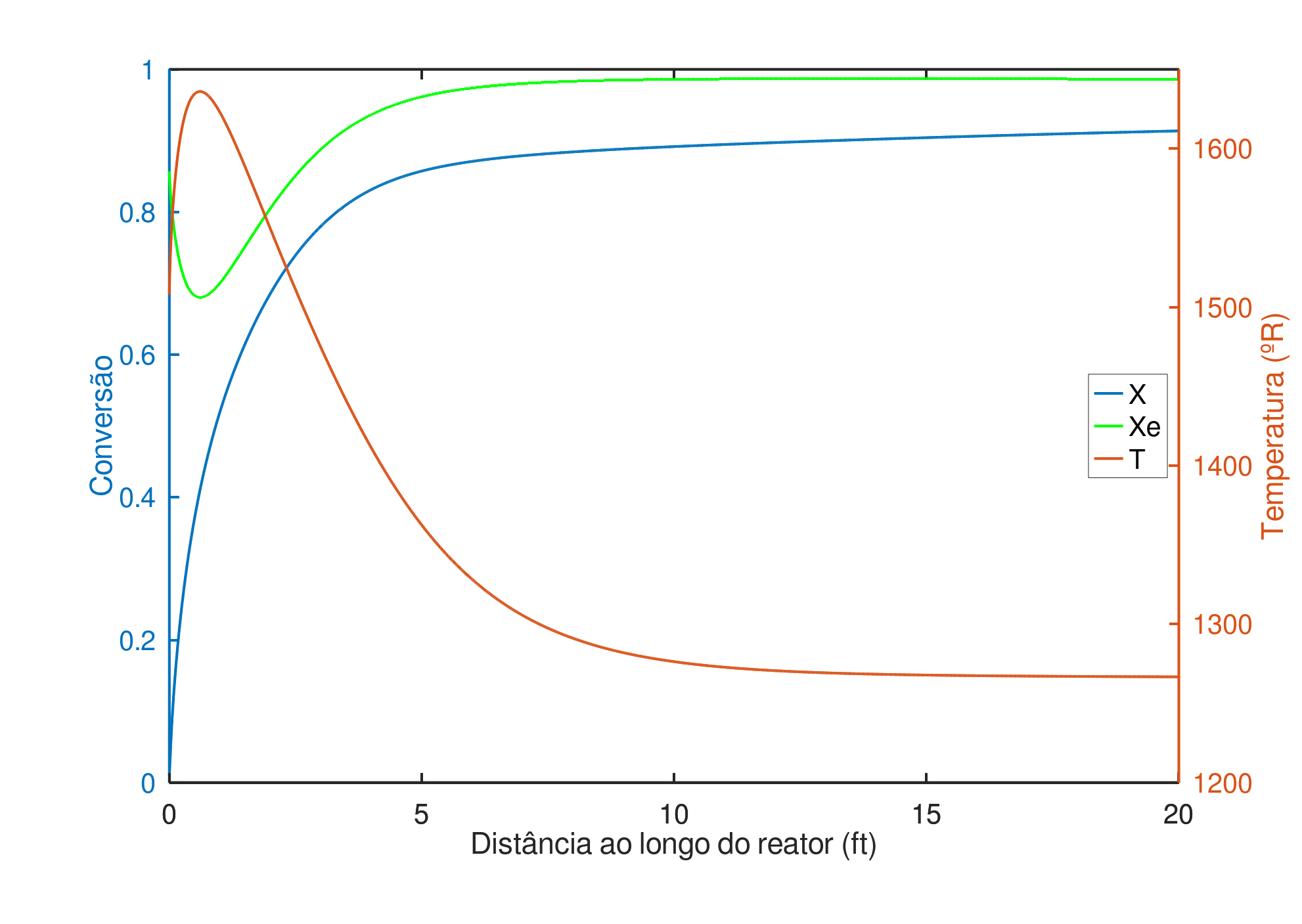
Aumentando a temperatura de alimentação para $1400 ^oR$, produz-se o gráfico da Figura 3. Preferível comparada à anterior, a conversão se aproxima mais da conversão de equilíbrio, sendo a conversão na saída 90,75% (98,60% é a conversão de equilíbrio). Nos primeiros $4 ft$ do reator a conversão já atinge 91% de seu valor final, isto ocorre pois nesta região a reação se aproxima do equilíbrio.

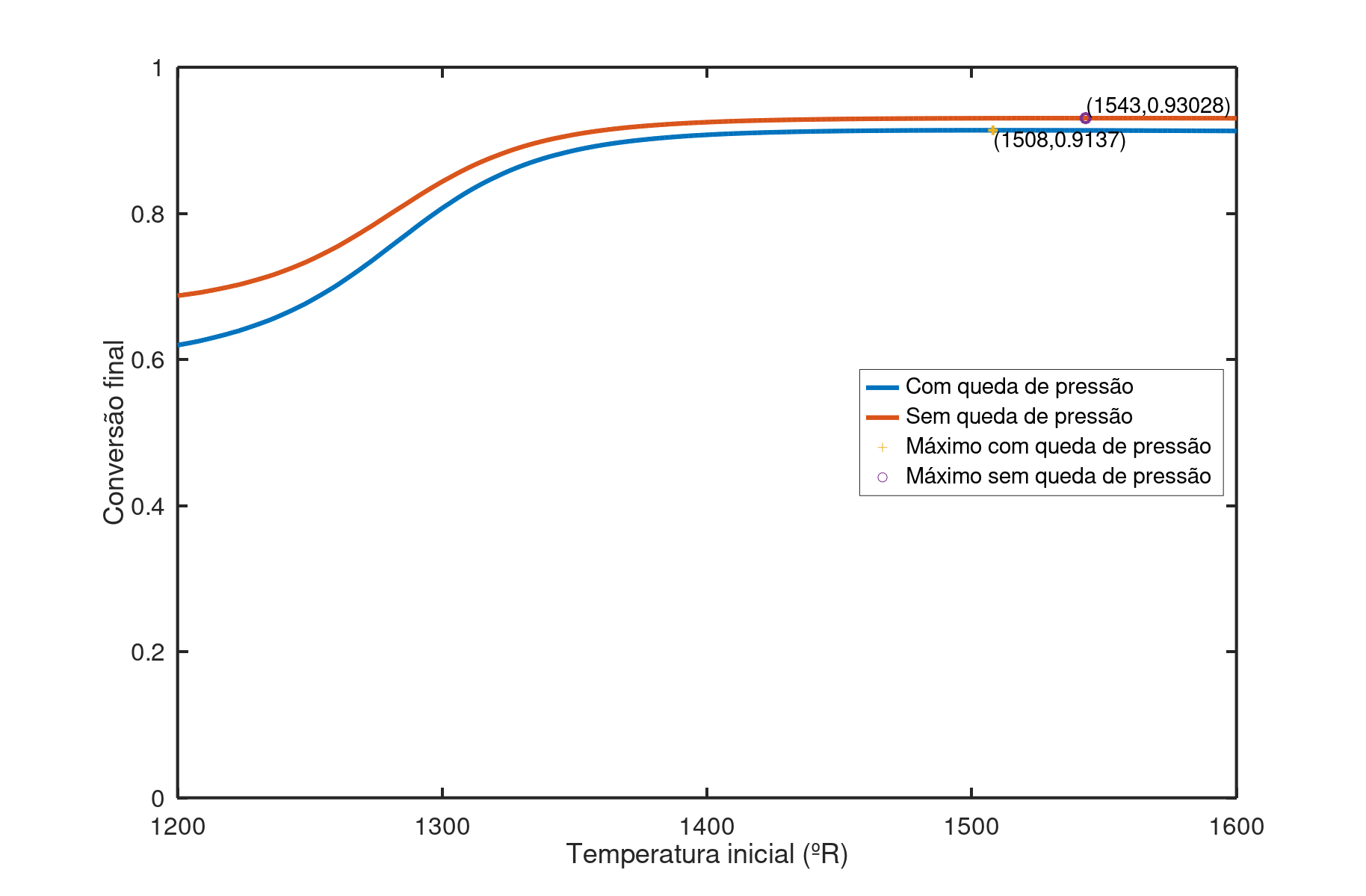
Confeccionando um gráfico da conversão final em função da temperatura inicial de $1200 ^oR$ a $1600 ^oR$ (Figura 4), encontra-se que a conversão é máxima (91,37%) quando a temperatura de alimentação é de $1508 ^oR$. Se os termos de queda de pressão são removidos a temperatura ótima de alimentação é elevada para $1543 ^oR$, com conversão de 93,03%. A temperatura máxima na qual a lei de velocidade é válida é $1489 ^oR$, ambas as máximas encontradas são superiores ao limite mas muito próximas. Dentro do intervalo de validade da lei de velocidade as curvas da conversão contra a temperatura de alimentação são exclusivamente crescentes e não há ponto de máximo, os pontos máximos na Figura 4 foram encontrados apenas após o intervalo de busca ser expandido.

Identificada a temperatura ótima de alimentação de $1508 ^oR$, podemos produzir o gráfico da Figura 5, com os perfis de temperatura e conversão. A conversão final é 91,37% e, semelhante às Figuras 2 e 3, a conversão de equilíbrio cai para um mínimo de 68% em $0,57 ft$, devido ao aumento brusco na temperatura até um máximo de $1636 ^oR$, quando a concentração do produto já é alta o suficiente para que a reação inversa se torne importante.

O autor ¹ nos informa que a temperatura não deve exceder $1585 ^oR$ em nenhum ponto do reator, devido a sinterização do catalisador. Respeitando esta restrição, não será possível operar o reator na temperatura ótima de alimentação, pois dos $0,13 ft$ aos $1,55 ft$ a temperatura excede o limite.

Para finalizar, a máxima temperatura de entrada possível é $1435 ^oR$, $73 ^oR$ abaixo da temperatura que produz a máxima conversão global. Mas se compararmos as conversões de saída obtidas nas duas temperaturas, 91,37% para a aquela e 91,18% para esta, percebe-se que o aumento na conversão é diminuto, e não há grandes perdas se a alimentação for realizada a $1435 ^oR$. Ainda limitada pela conversão de equilíbrio, nesta temperatura de entrada, 90% da conversão é atingida nos primeiros $3,67 ft$ do reator.

Conclusão Link para o cabeçalho

Desenvolveram-se todos os balanços necessários para simular o comportamento de reator de leito fixo não adiabático usado na produção de trióxido de enxofre. Encontrou-se uma temperatura ótima de alimentação de $1508 ^oR$, contudo, esta temperatura causa pontos quentes no reator que excedem os limites suportados pelo leito, sendo a máxima temperatura de alimentação permitida $1435 ^oR$. Observou-se também que a reação é limitada pelo equilíbrio termodinâmico, com 90% da conversão de saída (na temperatura de alimentação de $1435 ^oR$), obtida nos primeiros $3,67 ft$ do reator.

Referências Link para o cabeçalho